Fisher Discriminant Analysis (FDA)


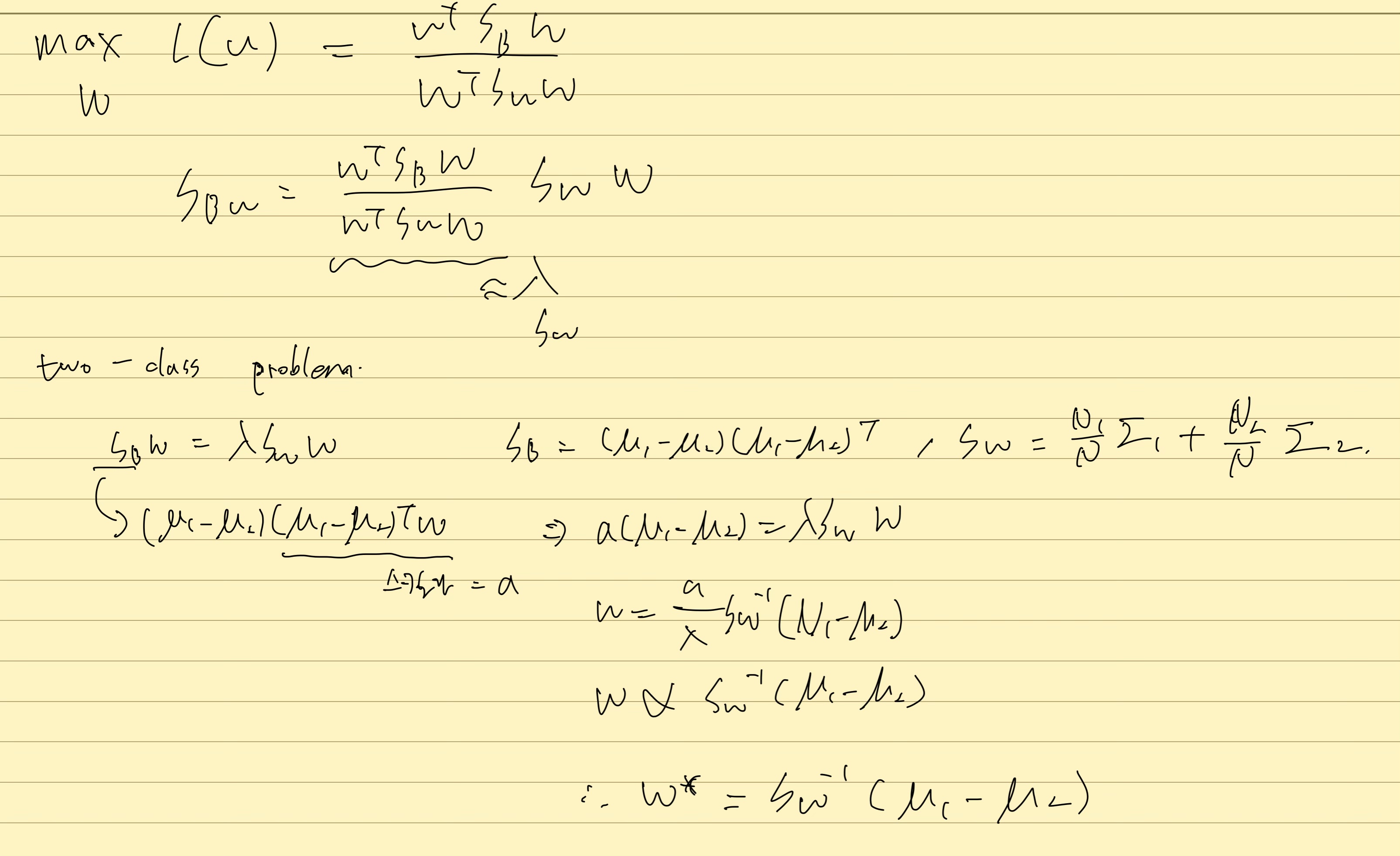
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# generating data set
n0 = 200
n1 = 200
sigma = \[\[0.9, -0.4\],
\[-0.4, 0.3\]\]
np.random.seed(0)
x0 = np.random.multivariate\_normal(\[2.5,2.5\], sigma, n0) # data in class 0
x1 = np.random.multivariate\_normal(\[1,1\], sigma, n1) # data in class 1
print(x0.shape)
print(x1.shape)
(200, 2) (200, 2)
mu0 = np.mean(x0, axis = 0)
mu1 = np.mean(x1, axis = 0)
S0 = np.dot((x0-mu0).T, x0-mu0)/(n0-1)
S1 = np.dot((x1-mu1).T, x1-mu1)/(n1-1)
w = np.linalg.solve(n0/(n0+n1)\*S0 + n1/(n0+n1)\*S1, mu0 - mu1)
print(w)
[ 9.64218334 18.00307461]
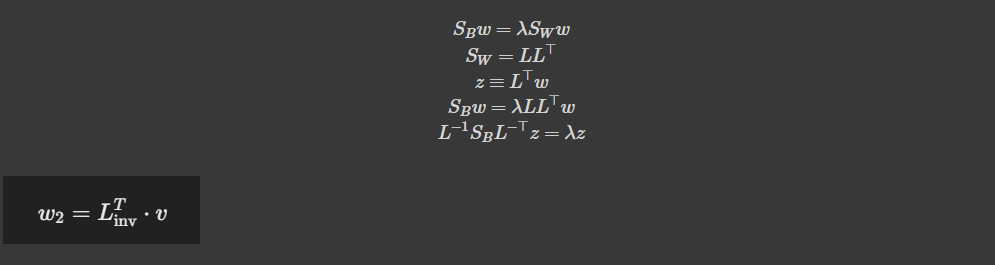
dmu = (mu0 - mu1)\[:,np.newaxis\]
Sb = np.dot(dmu, dmu.T)
#print(Sb.shape)
Sw = n0/(n0+n1)\*S0 + n1/(n0+n1)\*S1
L = np.linalg.cholesky(Sw)
#print(L)
print(np.allclose(Sw, np.dot(L,L.T)))
L\_inv = np.linalg.inv(L)
Sb\_new = np.dot(np.dot(L\_inv, Sb), L\_inv.T)
eigenvalues, eigenvectors = np.linalg.eigh(Sb\_new)
print(eigenvalues)
print(eigenvectors)
w2 = np.dot(L\_inv.T, eigenvectors\[:,-1:\])
print(np.dot(np.dot(w2.T, Sb), w2) / np.dot(np.dot(w2.T, Sw), w2))
print(w/w2\[:,0\])True
[ 0. 42.37927574]
[[-0.97005478 0.24288622]
[ 0.24288622 0.97005478]]
[[42.37927574]]
[6.50993669 6.50993669]
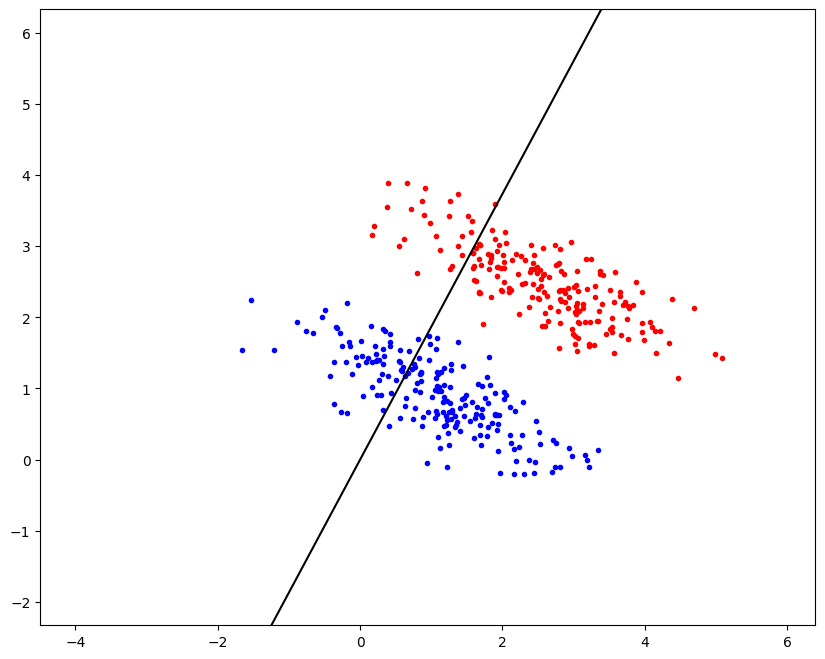
plt.figure(figsize = (10, 8))
plt.plot(x0\[:,0\], x0\[:,1\], 'r.')
plt.plot(x1\[:,0\], x1\[:,1\], 'b.')
xp = np.arange(-4, 6, 0.1)
yp = w\[1\]/w\[0\]\*xp
plt.plot(xp, yp, 'k')
plt.axis('equal')
plt.ylim(\[-2, 6\])
plt.show()
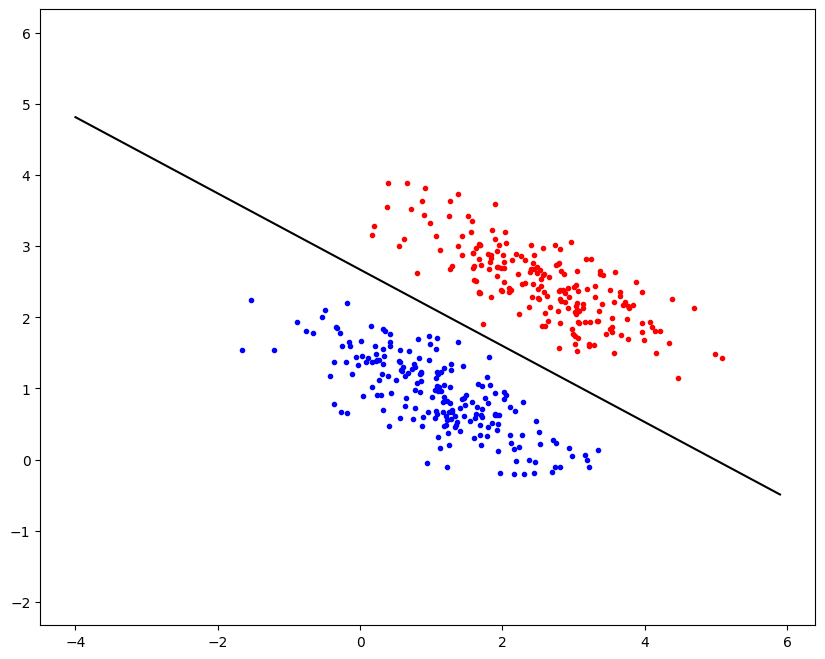
thres = np.sum(w \* 1/2 \* (mu1+mu0))
plt.figure(figsize = (10, 8))
plt.plot(x0\[:,0\], x0\[:,1\], 'r.')
plt.plot(x1\[:,0\], x1\[:,1\], 'b.')
xp = np.arange(-4, 6, 0.1)
yp = (thres - w\[0\] \* xp)/w\[1\]
plt.plot(xp, yp, 'k')
plt.axis('equal')
plt.ylim(\[-2, 6\])
plt.show()
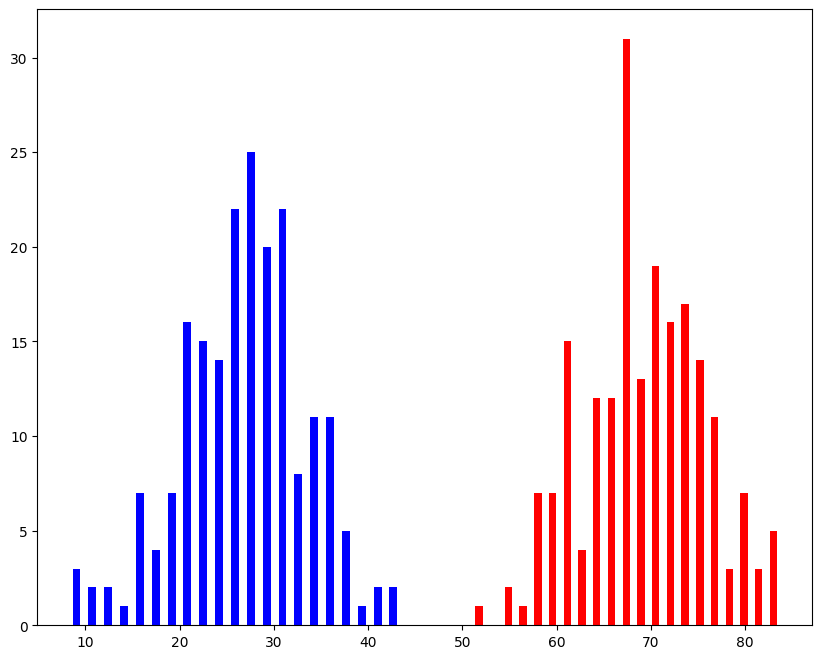
y1 = np.dot(x0,w)
y2 = np.dot(x1,w)
plt.figure(figsize = (10, 8))
plt.hist(y1, 21, color = 'r', rwidth = 0.5)
plt.hist(y2, 21, color = 'b', rwidth = 0.5)
plt.show()
Scikit-learn
\# reshape data
X = np.vstack(\[x0, x1\])
y = np.vstack(\[np.ones(\[n0, 1\]), np.zeros(\[n1, 1\])\])
from sklearn import discriminant\_analysis
clf = discriminant\_analysis.LinearDiscriminantAnalysis()
clf.fit(X, np.ravel(y))

\# projection
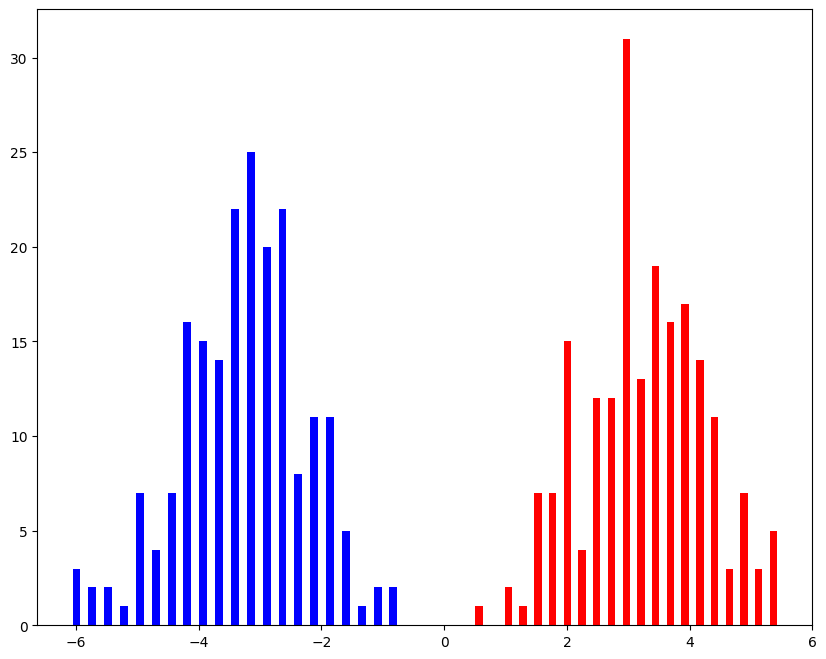
X\_LDA = clf.transform(X)
plt.figure(figsize = (10, 8))
plt.hist(X\_LDA\[0:200\], 21, color = 'r', rwidth = 0.5)
plt.hist(X\_LDA\[200:400\], 21, color = 'b', rwidth = 0.5)
plt.show()
clf.coef\_, clf.intercept\_
(array([[ 9.64218334, 18.00307461]]), array([-48.06306799]))
clf.coef\_/w, thres
(array([[1., 1.]]), 48.06306799151288)
'AI > 대학원' 카테고리의 다른 글
| 한양대학교 인공지능융합대학원 25년도 전기 신입생 모집 (10) | 2024.11.07 |
|---|---|
| Ridge Regression 실습 및 개념정리 (3) | 2024.11.01 |
| Going Deeper with Embedded FPGA Platform for Convolutional Neural Network 리뷰 (11) | 2024.10.27 |
| Autoencoder 정리 및 코드 구현 (1) | 2024.10.16 |
| PCA 정리 및 코드 구현 (0) | 2024.10.15 |



