개요
AI 프로그래밍 과제에서 나온 Ridge Regression 에 대한 문제 풀이 과정과 code 를 작성하고 결과를 해석 하여 의미를 살펴 본다.
Ridge Regression의 핵심 개념을 이해하고, 모델 피팅 시 정규화가 얼마나 중요한 역할을 하는지를 알아 보고 정규화 없이 과적합된 모델과 정규화를 추가하여 일반화된 모델 간의 성능 차이를 시각화하고 비교하는 것이 목표이다.
문제 설명
합성 데이터 세트에 대해 Ridge Regression(또는 Tikhonov 정규화)을 사용하여 analytic solution 으로 다항식 곡선을 맞추는 내용이다. 해당 모델과 loss 함수는 아래 과정을 참고 바란다.

import numpy as np
from matplotlib import pyplot as plt
import time
np.random.seed(1)
# train, test 데이터 생성 함수
def generate_data(N, a, b, c, d, std):
x = np.random.rand(N)
y = a*x**3 + b*x**2 + c*x + d + std*np.random.randn(N)
return x, y# train, test 데이터 생성
N_train = 10
N_test = 1000
a = 2.
b = 5.
c = -3
d = 6.
std = 0.02
x_train, y_train = generate_data(N_train, a, b, c, d, std)
x_test, y_test = generate_data(N_test, a, b, c, d, std)
x_clean = np.linspace(0,1,100)
# 생성된 data shape 확인
print(x_train.shape)
print(y_train.shape)
# train, test 데이터 분포 확인
plt.scatter(x_test, y_test, label='test')
plt.scatter(x_train, y_train, label='train')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')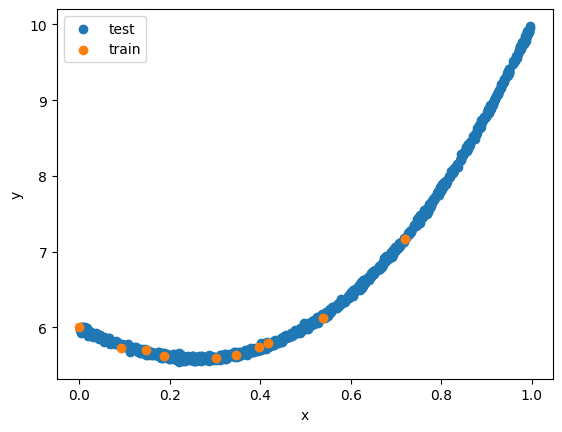

def getX(x, p):
X = np.ones((p+1, len(x)))
for i in range(p+1):
X[i] = x**(p-i)
return X
# without regularization
start = time.time()
for i in range(100000):
w1 = np.linalg.solve(XXT, Xy) # 좀 더 빠르다.
print(time.time() - start)
start = time.time()
for i in range(100000):
XXT_inv = np.linalg.inv(XXT)
w2 = np.dot(XXT_inv, Xy)
print(time.time() - start)
print(np.allclose(w1, w2))
print(w1.shape, w2.shape)
X_predict = getX(x_clean, p)
y_predict = np.dot(X_predict.T, w1)
plt.scatter(x_test, y_test, label='test')
plt.scatter(x_train, y_train, label='train')
plt.plot(x_clean, y_predict, c='r', label='model')
plt.ylim([y_test.min()-0.1, y_test.max()+0.1])
plt.legend()
Solve for different degrees of polynomials
def curve_fitting(x, y, p, alpha):
X = getX(x, p) # X는 다항식 특성을 생성하는 함수 (예를 들어, p차 다항식)
XXT = np.dot(X, X.T) # X와 X의 전치 행렬 곱
I = np.eye(XXT.shape[0]) # I는 XXT와 같은 크기의 항등 행렬
Xy = np.dot(X, y) # X와 y의 행렬 곱
# regularization αI를 추가하여 ridge regression 사용
w = np.linalg.solve(XXT + alpha * I, Xy) # (XXT + αI)^{-1} Xy
# 훈련 데이터에 대한 에러 계산 (MSE)
train_error = np.mean((np.dot(X.T, w) - y) ** 2) # MSE
return w, train_error
def predict(x_predict, w):
p = len(w)-1
X_predict = getX(x_predict, p)
return np.dot(X_predict.T, w)
def get_test_error(x_test, y_test, w):
y_predict = predict(x_test, w)
return np.mean((y_predict - y_test)**2)
def plot_result(x_train, y_train, w):
plt.scatter(x_train, y_train, label='train')
x_clean = np.linspace(0,1,100)
y_predict = predict(x_clean, w)
plt.plot(x_clean, y_predict, label='model', c='g')
plt.ylim([y_test.min()-0.1, y_test.max()+0.1])
plt.legend()
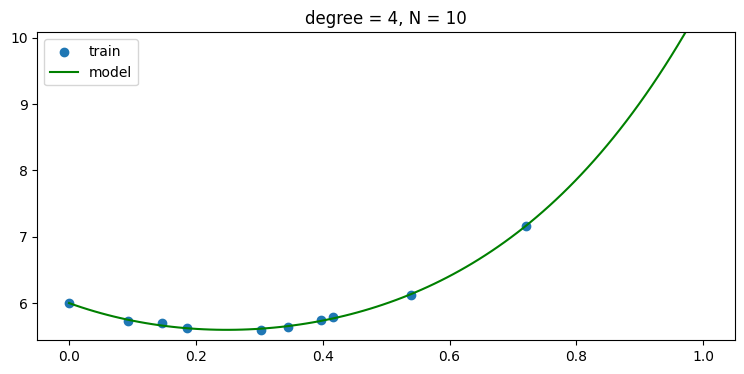
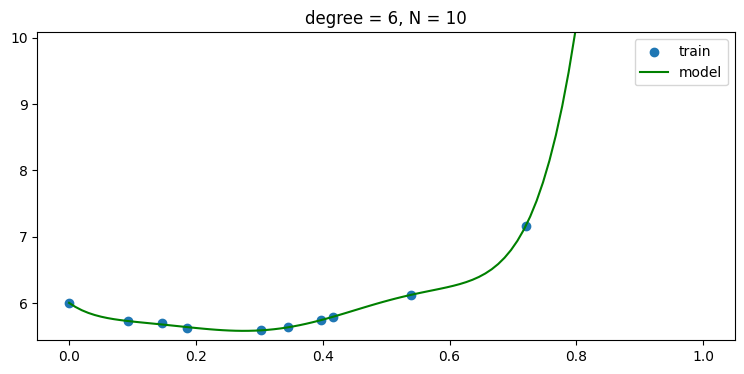
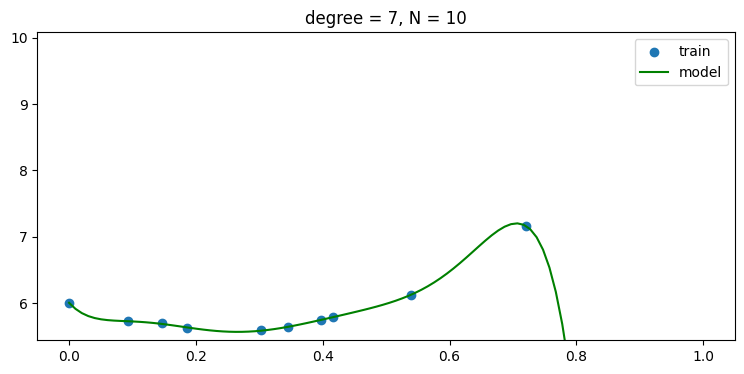
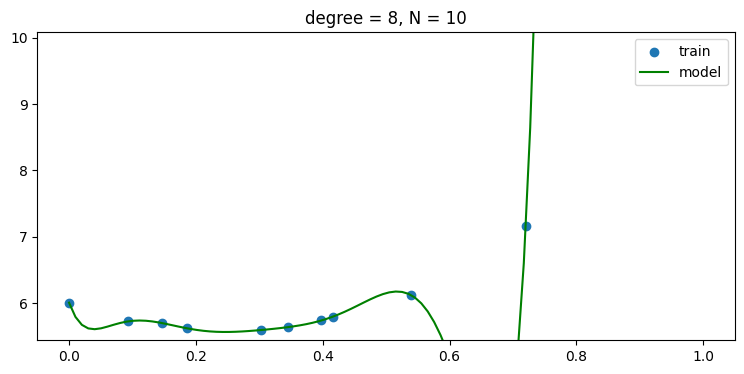
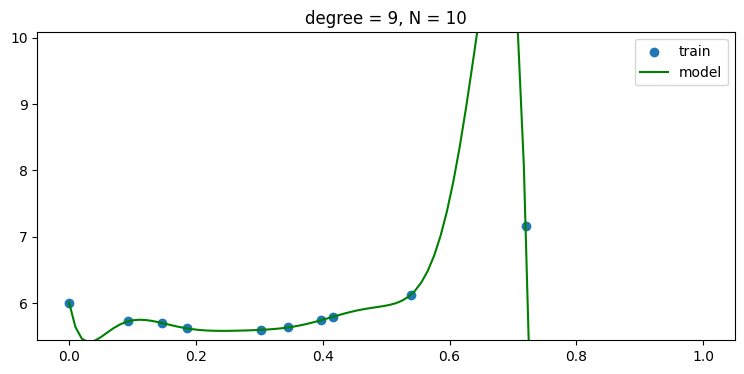
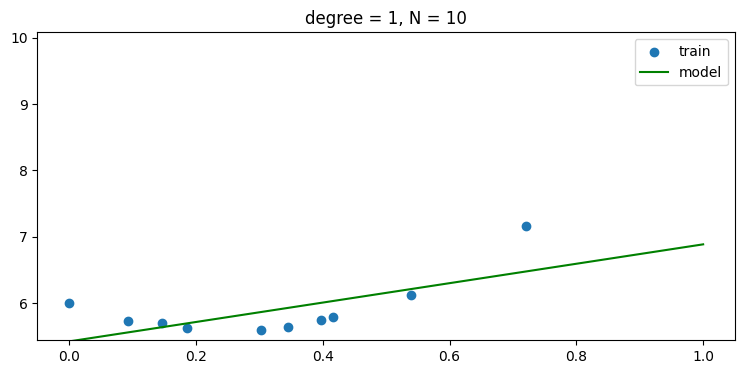
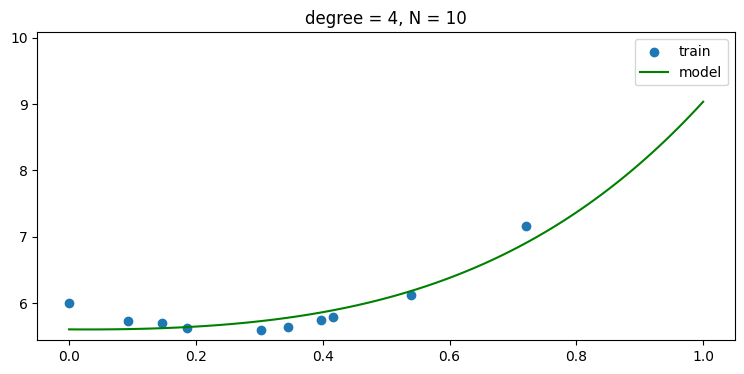
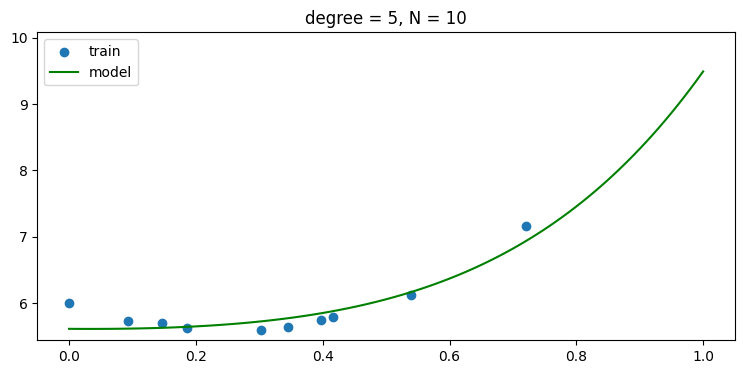
plt.title('degree = {:d}, N = {:d}'.format(len(w)-1, len(x_train)))without regularization, i.e., use α = 0
- regularization 을 사용하지 않을 경우 데이터 숫자가 적어 차수가 높아 질 수록 오버피팅 현상이 나타남을 그래프를 통해 알 수 있다.
train_error_list = []
test_error_list = []
w_list = []
max_polynomial = 10
alpha = 0 # without regularization
for p in range(max_polynomial+1):
w, train_error = curve_fitting(x_train, y_train, p, alpha)
test_error = get_test_error(x_test, y_test, w)
train_error_list.append(train_error)
test_error_list.append(test_error)
w_list.append(w)
plt.figure(figsize=(9, 4))
plot_result(x_train, y_train, w)





p_list = np.arange(N_train)
N_disp = 6
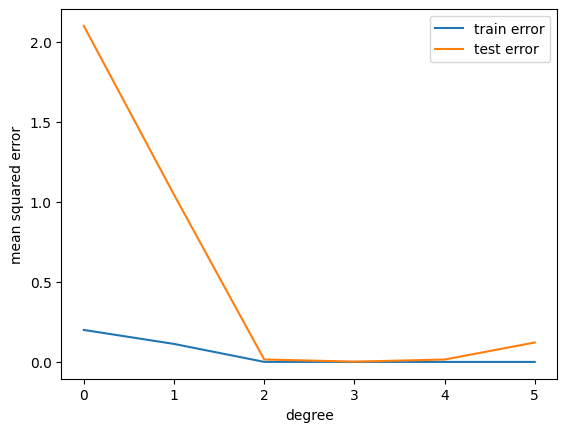
plt.plot(p_list[:N_disp], train_error_list[:N_disp], label='train error')
plt.plot(p_list[:N_disp], test_error_list[:N_disp], label='test error')
plt.xlabel('degree')
plt.ylabel('mean squared error')
plt.legend()
using regularization, i.e., use α > 0
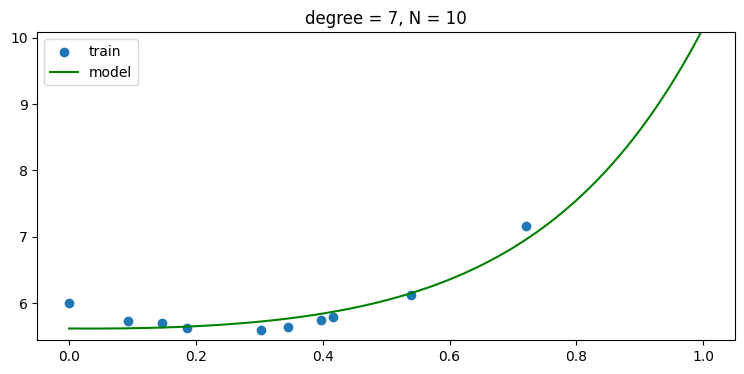
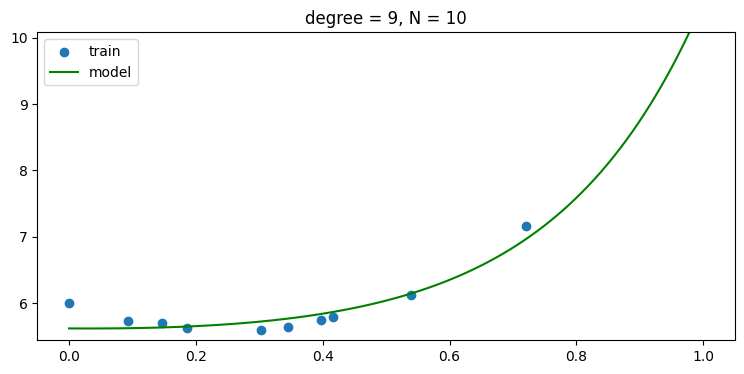
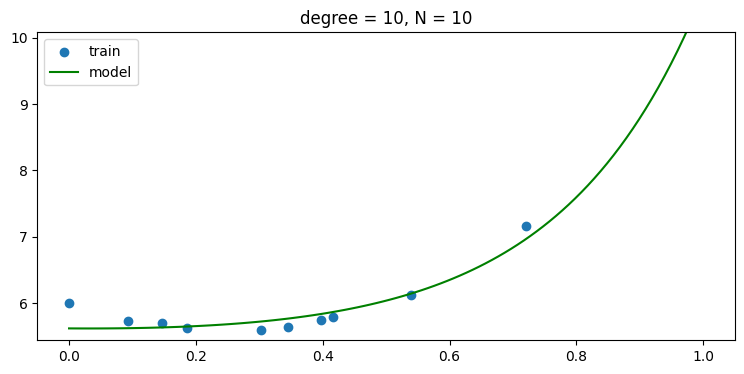
- regularization 을 사용하면 오버피팅에 강인해져 6차항 이상에서도 모델이 학습을 잘 해서 test error 가 높아 지지 않음을 볼 수 있다.
train_error_list_with_ridge = []
test_error_list_with_ridge = []
w_list_with_ridge = []
max_polynomial = 10
alpha = 0.05 # using regularization
for p in range(max_polynomial+1):
w, train_error = curve_fitting(x_train, y_train, p, alpha)
test_error = get_test_error(x_test, y_test, w)
train_error_list_with_ridge.append(train_error)
test_error_list_with_ridge.append(test_error)
w_list_with_ridge.append(w)
plt.figure(figsize=(9, 4))
plot_result(x_train, y_train, w)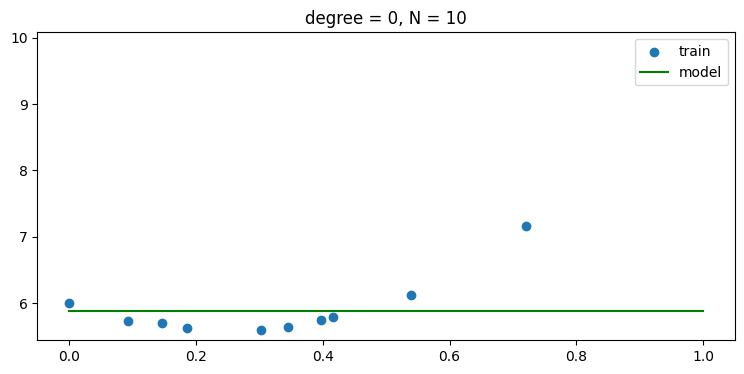




p_list_with_ridge = np.arange(N_train)
N_disp = max_polynomial
plt.plot(p_list_with_ridge[:N_disp], train_error_list_with_ridge[:N_disp], label='train error')
plt.plot(p_list_with_ridge[:N_disp], test_error_list_with_ridge[:N_disp], label='test error')
plt.xlabel('degree')
plt.ylabel('mean squared error with ridge regression')
plt.legend()
How do the results vary as α increases?
- α가 작은 값일 때는 정규화의 영향이 거의 없기 때문에, 모델이 데이터를 더 복잡하게 맞추려고 하며 이는 모델이 overfitting 될 가능성을 높임
- 너무 큰 α 값은 underfitting 을 일으킬 수 있으며 이는 모델이 너무 단순해져서 훈련과 테스트 모두에서 성능이 저하가 나타날 수 있음
train_error_list_with_ridge = {}
test_error_list_with_ridge = {}
w_list_with_ridge = {}
alphas = [0.00001, 0.05, 0.1, 0.8] # alpha 값 리스트
max_polynomial = 10 # 다항식 차수는 0부터 10까지
# 각 alpha에 대한 에러 결과를 저장할 리스트 초기화
for alpha in alphas:
train_error_list_with_ridge[alpha] = []
test_error_list_with_ridge[alpha] = []
w_list_with_ridge[alpha] = []
# 각 alpha 값에 대해 여러 다항식 차수를 학습하고 테스트
for alpha in alphas:
for p in range(max_polynomial + 1):
w, train_error = curve_fitting(x_train, y_train, p, alpha)
test_error = get_test_error(x_test, y_test, w)
# 각 alpha 값에 대한 훈련 및 테스트 에러 저장
train_error_list_with_ridge[alpha].append(train_error)
test_error_list_with_ridge[alpha].append(test_error)
w_list_with_ridge[alpha].append(w)
# 모델 학습 결과 시각화
# 출력 이미지가 너무 많아서 주석 처리
# 주석 풀고 확인 가능
# plt.figure(figsize=(9, 4))
# plot_result(x_train, y_train, w)
# plt.title(f"Ridge Regression with polynomial={p}, alpha={alpha}")
# plt.show()
# 결과를 비교하는 코드 (테스트 에러에 대한 플롯)
plt.figure(figsize=(10, 6))
for alpha in alphas:
plt.plot(range(max_polynomial + 1), test_error_list_with_ridge[alpha], label=f'alpha={alpha}')
plt.xlabel('polynomial degree')
plt.ylabel('mean squared error (test)')
plt.legend()
plt.title('Test Error for different alpha values')
plt.show()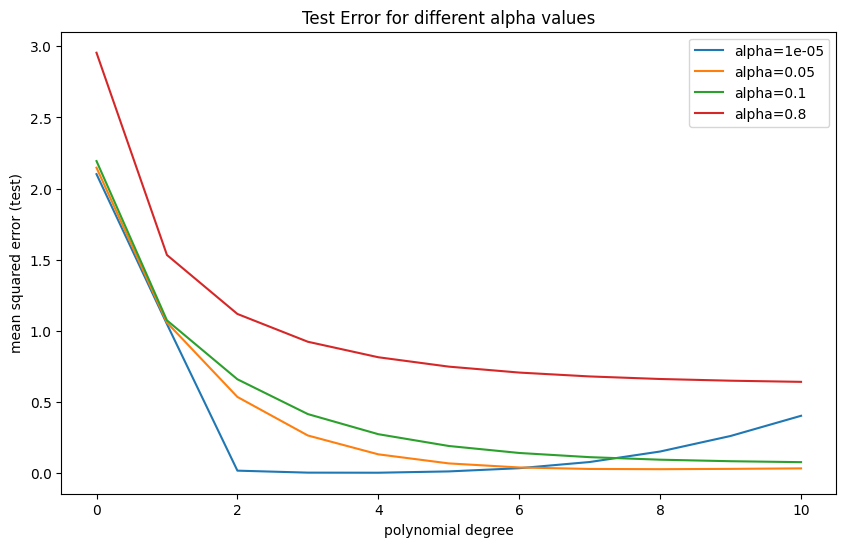
- 파란색 (alpha=1e-05): regularization 이 거의 없는 상태로, 다항식 차수가 증가할수록 초반에는 에러가 줄어들지만, 이후 다시 에러가 증가하는 모습을 보입니다. 이는 overfitting 의 징후로, 차수가 너무 높아지면 모델이 훈련 데이터에 과도하게 맞추어져 테스트 데이터에서의 성능이 떨어집니다.
- 주황색 (alpha=0.05): 적당한 regularization 이 적용된 상태로, 차수가 증가할수록 에러가 점점 줄어들다가 거의 일정하게 유지됩니다. 테스트 에러가 가장 안정적으로 낮은 값을 유지하고 있습니다.
- 초록색 (alpha=0.1): 이 곡선도 유사하게 테스트 에러가 점차 줄어들며 안정적입니다. 다소 강한 정규화가 적용된 상태입니다.
- 빨간색 (alpha=0.8): 큰 α 값에서는 에러가 높은 상태로 유지됩니다. 이는 underfitting 상태를 나타내며, 모델이 데이터의 중요한 패턴을 포착하지 못하고 단순화된 모델을 만들고 있습니다.
추가 : Ridge regularization 의 핵심 개념

Ridge regularization 정규화의 효과

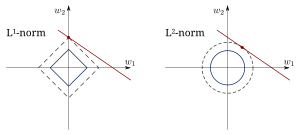
Ridge와 Lasso의 비교

'AI > 대학원' 카테고리의 다른 글
| 도메인에 맞는 AI 지능화 전략 (자율주행 보안) (7) | 2024.11.10 |
|---|---|
| 한양대학교 인공지능융합대학원 25년도 전기 신입생 모집 (11) | 2024.11.07 |
| Going Deeper with Embedded FPGA Platform for Convolutional Neural Network 리뷰 (11) | 2024.10.27 |
| FDA 정리 및 코드 구현 (3) | 2024.10.16 |
| Autoencoder 정리 및 코드 구현 (2) | 2024.10.16 |