PCA의 주요 개념
- 분산(Variance): 데이터가 얼마나 퍼져 있는지를 나타내며, PCA는 분산이 큰 방향(즉, 정보가 많이 있는 방향)을 찾습니다.
- 주성분(Principal Component): 분산이 가장 큰 방향의 벡터입니다. 첫 번째 주성분은 가장 많은 분산을 설명하고, 두 번째 주성분은 그다음으로 많은 분산을 설명하며, 서로 직교합니다.
- 공분산 행렬(Covariance Matrix): 각 변수 간의 상관관계를 나타내는 행렬로, 이 행렬의 고유벡터(eigenvector)를 통해 주성분을 구합니다.
- 고유벡터와 고유값(Eigenvectors and Eigenvalues): 공분산 행렬에서 고유벡터는 주성분의 방향을, 고유값은 각 주성분이 설명하는 분산의 크기를 의미합니다.
PCA의 장점
- 차원 축소: 고차원 데이터를 저차원으로 축소하여 계산량을 줄입니다.
- 데이터 시각화: 2D 또는 3D로 차원 축소하여 데이터를 시각적으로 분석할 수 있습니다.
- 노이즈 제거: 중요하지 않은 변동(노이즈)을 제거하고, 주요 정보를 남길 수 있습니다.
PCA의 단점
- 선형성 가정: PCA는 선형 관계를 가정하므로 비선형 관계를 잘 처리하지 못합니다.
- 설명력 감소: 너무 많은 차원을 축소하면 데이터의 중요한 정보를 잃을 수 있습니다.

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# data generation
np.random.seed(0)
num_data = 5000
mean = np.array([0, 0]) # zero-mean
cov = np.array([[3, 1.5],
[1.5, 1]])
X = np.random.multivariate_normal(mean, cov, num_data)
fig = plt.figure(figsize = (10, 8))
plt.plot(X[:,0], X[:,1], 'k.', alpha = 0.3)
plt.axis('equal')
plt.grid(alpha = 0.3)
plt.show()

mean_X = np.mean(X, axis=0)
S = 1/(num_data-1)*np.dot((X - mean_X).T, X - mean_X) # 2*2 matrix
D, U = np.linalg.eigh(S)
idx = np.argsort(-D) # argsort sorts in ascending order
D = D[idx]
U = U[:,idx]
print(D, '\n') # lamda1, lamda2 (eigen value)
print(U) # each column vector is u1, u2 (eigen vector coresponds to each eigen value)
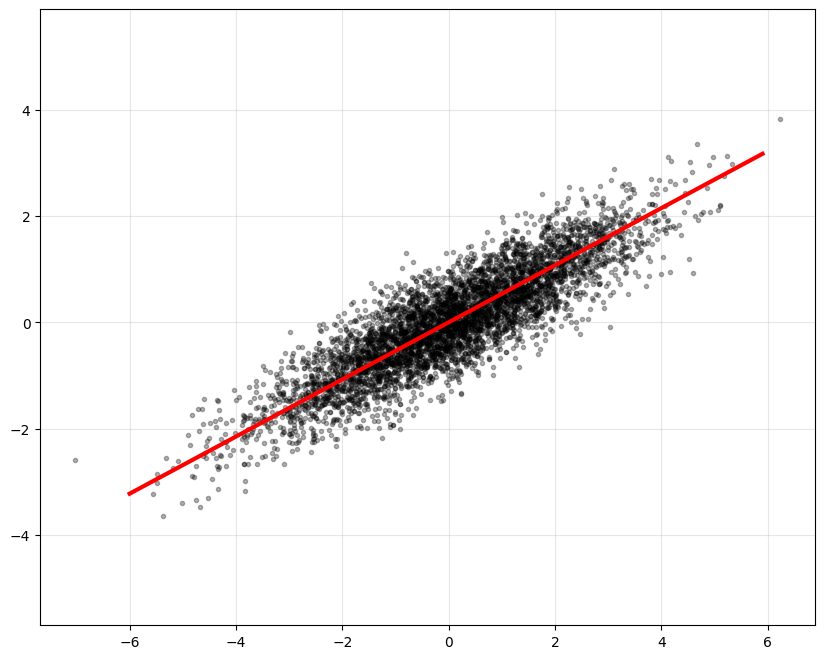
# for plotting u1
h = U[1,0]/U[0,0] # calculate slope
xp = np.arange(-6, 6, 0.1)
yp = h*xp
fig = plt.figure(figsize = (10, 8))
plt.plot(X[:,0], X[:,1], 'k.', alpha = 0.3)
plt.plot(xp, yp, 'r', linewidth = 3)
plt.axis('equal')
plt.grid(alpha = 0.3)
plt.show()