 FDA 정리 및 코드 구현
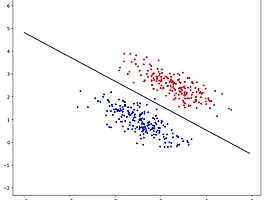
Fisher Discriminant Analysis (FDA)import numpy as npimport matplotlib.pyplot as plt%matplotlib inline# generating data set n0 = 200 n1 = 200 sigma = \[\[0.9, -0.4\], \[-0.4, 0.3\]\]np.random.seed(0)x0 = np.random.multivariate\_normal(\[2.5,2.5\], sigma, n0) # data in class 0x1 = np.random.multivariate\_normal(\[1,1\], sigma, n1) # data in class 1print(x0.shape)print(x1.shape)(200, 2..
FDA 정리 및 코드 구현
Fisher Discriminant Analysis (FDA)import numpy as npimport matplotlib.pyplot as plt%matplotlib inline# generating data set n0 = 200 n1 = 200 sigma = \[\[0.9, -0.4\], \[-0.4, 0.3\]\]np.random.seed(0)x0 = np.random.multivariate\_normal(\[2.5,2.5\], sigma, n0) # data in class 0x1 = np.random.multivariate\_normal(\[1,1\], sigma, n1) # data in class 1print(x0.shape)print(x1.shape)(200, 2..