개요
AI 프로그래밍 수업에서 배운 Gaussian processes 에 코드로 구현 한 내용을 정리 합니다.
개인적으로 GP 에 대해 아직 완전히 이해를 못하고 있는 부분들이 있어서 학습이 더 필요 할 거 같습니다.
https://en.wikipedia.org/wiki/Gaussian_process
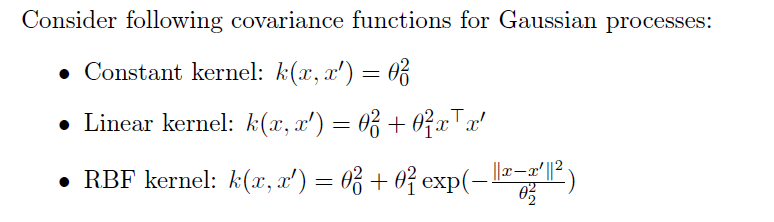
1. Gaussian processes visualize
- 평균 함수 m(x)=0m(x) = 0을 사용하고, 주어진 세 가지 커널 함수 각각을 사용해 Gaussian process를 설정합니다.
- 이 과정에서 매개변수를 다양하게 바꾸어가며 Gaussian process 에서 나오는 임의의 함수들을 샘플링합니다.
- 각 커널 함수가 샘플 함수의 행태에 미치는 영향을 시각적으로 보여주고, 이에 대해 논의합니다.
주어진 커널 함수 구현
# 각 커널 함수 정의
def constant_kernel(x1, x2, theta0):
# Constant kernel: k(x, x') = θ0^2
return theta0**2 * np.ones((x1.shape[0], x2.shape[0]))
def linear_kernel(x1, x2, theta0, theta1):
# Linear kernel: k(x, x') = θ0^2 + θ1^2 x^T x'
linear_part = theta1**2 * np.dot(x1, x2.T)
return theta0**2 + linear_part
def rbf_kernel(x1, x2, theta0, theta1, theta2):
# RBF kernel: k(x, x') = θ0^2 + θ1^2 * exp(-||x - x'||^2 / θ2^2)
dist_sq = np.sum(x1**2, axis=1).reshape(-1, 1) + np.sum(x2**2, axis=1).reshape(1, -1) - 2 * np.dot(x1, x2.T)
rbf_part = theta1**2 * np.exp(-1.0 * dist_sq / theta2**2)
return theta0**2 + rbf_part
시각화 함수 구현
# 시각화 함수 정의
def plot_gaussian_process_samples(kernel_func, theta_params, kernel_name, x_query, N_sample=5):
plt.figure(figsize=(10, 6))
for theta_set in theta_params:
# 커널 행렬 계산
if kernel_name == "Constant":
K = kernel_func(x_query[:, np.newaxis], x_query[:, np.newaxis], theta_set[0])
elif kernel_name == "Linear":
K = kernel_func(x_query[:, np.newaxis], x_query[:, np.newaxis], theta_set[0], theta_set[1])
elif kernel_name == "RBF":
K = kernel_func(x_query[:, np.newaxis], x_query[:, np.newaxis], theta_set[0], theta_set[1], theta_set[2])
# 평균 함수 및 샘플 함수 생성
mean_ftn = np.zeros(len(x_query))
y_sample = np.random.multivariate_normal(mean_ftn, K, N_sample)
# 샘플 함수 시각화
for i in range(N_sample):
plt.plot(x_query, y_sample[i]) # , label=f"Theta: {theta_set}")
plt.title(f"Gaussian Process Samples with {kernel_name} Kernel")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()
매개변수 설명
- kernel_func: 커널 함수입니다. 이 함수는 상수, 선형, RBF 커널 등 다양한 커널을 인자로 받을 수 있습니다. 이 함수는 가우시안 프로세스의 공분산 행렬을 정의하는 역할을 합니다.
- theta_params: 커널 함수에 사용될 매개변수들을 포함한 리스트입니다. 예를 들어, 상수 커널의 theta0, 선형 커널의 theta0와 theta1, RBF 커널의 theta0, theta1, theta2 등 각각의 커널에 필요한 파라미터들이 담겨있습니다.
- kernel_name: 커널의 종류입니다. "Constant", "Linear", "RBF" 등 세 가지 유형이 있습니다.
- x_query: Gaussian process 를 평가할 쿼리 지점들의 배열입니다. 예를 들어 x 축의 특정 지점들에 대해 가우시안 프로세스를 시각화할 때 사용됩니다.
커널 행렬 계산
- theta_params 리스트의 각 요소를 반복하면서 커널 매개변수 theta_set을 설정합니다.
- 각 커널의 이름에 따라 적절한 kernel_func을 호출하여 커널 행렬 K를 계산합니다.
- x_query[:, np.newaxis]를 사용하여 2차원 배열 형태로 변환합니다. 이는 커널 함수에서 브로드캐스팅을 사용해 모든 데이터 포인트 간의 관계를 계산할 수 있도록 하기 위함입니다.
- 예를 들어, x_query가 (n_samples,)인 1차원 배열일 경우 이를 (n_samples, 1) 형태로 변환합니다.
- K는 커널 행렬(또는 공분산 행렬)로, 각 데이터 포인트 간의 유사도 또는 공분산을 나타냅니다.
평균 함수 및 샘플 함수 생성
- mean_ftn = np.zeros(len(x_query)): 모든 x_query 지점에 대해 평균 함수를 0으로 설정합니다. 즉, 여기서는 평균이 0인 가우시안 프로세스를 생성합니다.
- y_sample = np.random.multivariate_normal(mean_ftn, K, N_sample):
- 평균이 mean_ftn이고 공분산이 K인 다변량 정규분포에서 N_sample 개수만큼의 샘플을 생성합니다.
- 생성된 y_sample의 크기는 (N_sample, len(x_query))로, N_sample 개의 샘플 함수들이 각 x_query 지점에서의 함수 값을 포함합니다.
Sample random functions
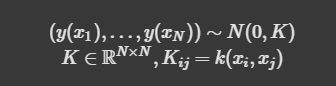
N_sample = 30
x_query = np.linspace(-1,11,101)
mean_ftn = np.zeros(len(x_query))# 하이퍼파라미터 설정
theta0_values = [0.5, 1.0, 2.0]
theta1_values = [0.5, 1.0, 2.0]
theta2_values = [0.5, 1.0, 2.0]
Constant Kernel
# Constant Kernel
constant_params = [(theta0,) for theta0 in theta0_values]
plot_gaussian_process_samples(constant_kernel, constant_params, "Constant", x_query)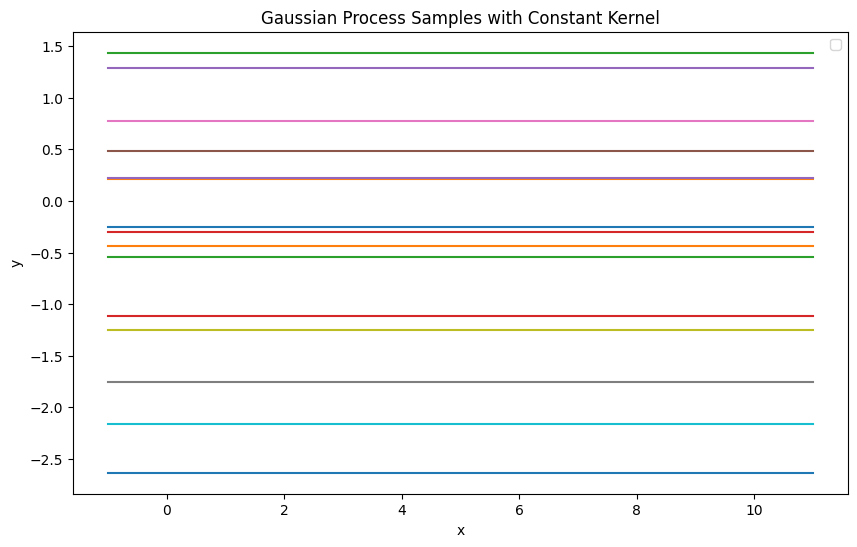
- theta0 값이 클수록 해당 함수 샘플의 높이가 증가 작을 수록 감소
- Constant Kernel 이 입력 지점 간의 관계를 무시하고 모든 지점에서 동일한 상수 값 가지도록 함
Linear Kernel
# Linear Kernel
linear_params = [(theta0, theta1) for theta0 in theta0_values for theta1 in theta1_values]
plot_gaussian_process_samples(linear_kernel, linear_params, "Linear", x_query)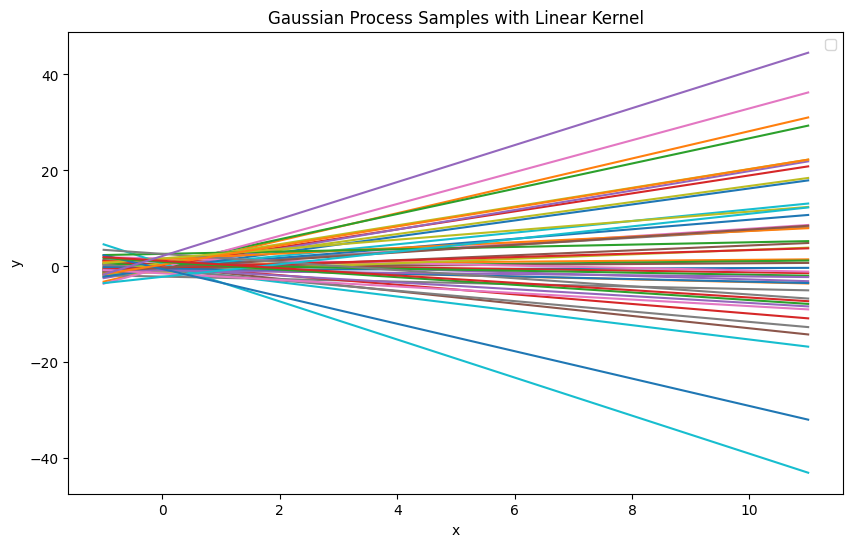
- theta0 그래프의 y-축에서의 초기 위치(오프셋)를 조절
- theta0 의 값이 증가하면, 모든 샘플 함수가 더 높은 값에서 시작
- theta1 그래프의 기울기를 조절
- theta1 의 값이 클수록 샘플 함수의 기울기 변화가 커져, x의 변화에 따라 y 값이 더 급격히 변함
RBF Kernel
# RBF Kernel
rbf_params = [(theta0, theta1, theta2) for theta0 in theta0_values for theta1 in theta1_values for theta2 in theta2_values]
plot_gaussian_process_samples(rbf_kernel, rbf_params, "RBF", x_query)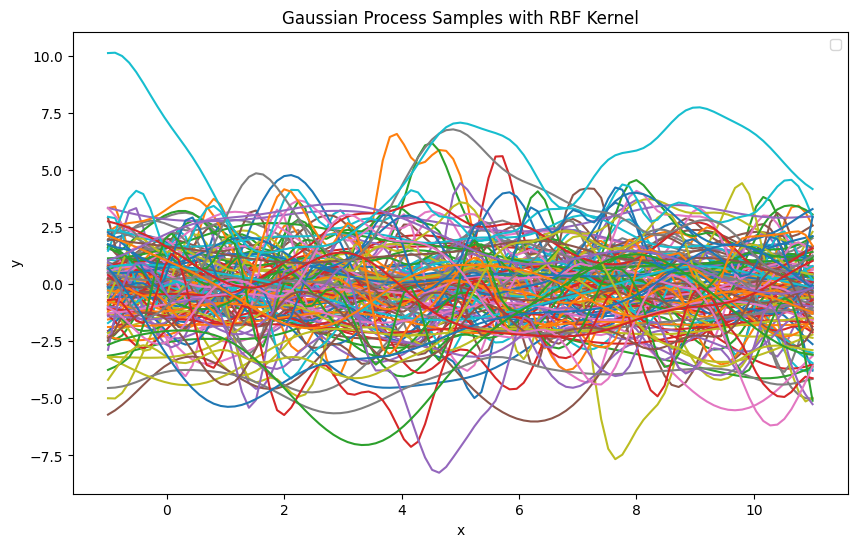
- theta0 그래프의 y-축 위치를 조정하는 상수 항
- theta1 값이 커질수록 함수의 진폭이 커져 더 크게 변화하는 곡선이 생성
- theta2 값이 작을수록 지점 간의 상관관계가 더 국소적이 되어 가까운 점들만 강한 상관관계를 가짐, 반대로 값이 면 더 넓은 범위의 지점들이 높은 상관관계를 가지게 되어 곡선이 더 완만해짐
2. Gaussian process regression
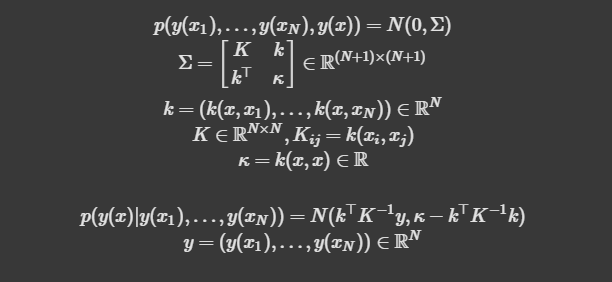
covariance function
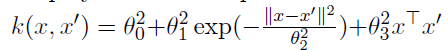
- 평균 함수 m(x)=0 과 주어진 covariance function를 사용하여 가우시안 프로세스를 설정합니다:
- 주어진 데이터 포인트를 사용해Gaussian process regression 를 수행합니다.
- 데이터 포인트: {(0,1),(0.1,0.6),(0.2,0.5),(0.3,−0.2),(0.4,0.2),(0.5,0.6),(0.6,0.8),(0.7,0.3),(0.8,0.3),(1.0,0.8)}
- 모델이 학습된 후, 입력 x∈[−0.5,1.5] 에 대해 예측 값을 시각화하고, 신뢰 구간 (즉, 예측 값 ± 1 표준편차)을 시각화합니다.
커널 함수 정의
# 커널 함수 정의
def custom_kernel(x1, x2, theta0, theta1, theta2, theta3):
# k(x, x') = θ0^2 + θ1^2 * exp(-||x - x'||^2 / θ2^2) + θ3^2 x^T x'
# RBF
dist_sq = np.sum(x1**2, axis=1).reshape(-1, 1) + np.sum(x2**2, axis=1).reshape(1, -1) - 2 * np.dot(x1, x2.T)
rbf_part = theta1**2 * np.exp(-1.0 * dist_sq / theta2**2)
# 선형 부분
linear_part = theta3**2 * np.dot(x1, x2.T)
return theta0**2 + rbf_part + linear_part
Gaussian process regression 함수 구현
# 가우시안 프로세스 회귀 함수 정의
def GPregression(x, y, x_query, kernel, theta_params):
theta0, theta1, theta2, theta3 = theta_params
K = kernel(x[:, np.newaxis], x[:, np.newaxis], theta0, theta1, theta2, theta3)
k = kernel(x[:, np.newaxis], x_query[:, np.newaxis], theta0, theta1, theta2, theta3)
kappa = kernel(x_query[:, np.newaxis], x_query[:, np.newaxis], theta0, theta1, theta2, theta3)
K_inv = np.linalg.inv(K + 1e-8 * np.eye(len(x))) # 노이즈 추가하여 역행렬 안정화
mean = np.dot(k.T, np.dot(K_inv, y[:, np.newaxis])).flatten()
cov = kappa - np.dot(np.dot(k.T, K_inv), k)
return mean, cov
주어진 데이터 포인트 생성
# 주어진 데이터 포인트
x_train = np.array([0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 1.0])
y_train = np.array([1.0, 0.6, 0.5, -0.2, 0.2, 0.6, 0.8, 0.3, 0.3, 0.8])
# 예측할 x 범위
x_query = np.linspace(-0.5, 1.5, 100)
# 하이퍼파라미터 설정
theta_params = (1.0, 1.0, 0.2, 0.5) # (theta0, theta1, theta2, theta3)
예측 수행 및 시각화
# 예측 수행
mean_ftn, cov_ftn = GPregression(x_train, y_train, x_query, custom_kernel, theta_params)
std = np.sqrt(np.diag(cov_ftn)) # 분산의 제곱근으로 표준 편차 계산
# 결과 시각화
plt.figure(figsize=(10, 6))
plt.plot(x_train, y_train, 'ro', label='Training Data')
plt.plot(x_query, mean_ftn, 'b-', label='Prediction Mean')
plt.fill_between(x_query, mean_ftn.ravel() - std, mean_ftn.ravel() + std, alpha=0.5, label='Confidence Interval')
plt.xlabel('x', fontsize=15)
plt.ylabel('y', fontsize=15)
plt.title('Gaussian Process Regression with Custom Kernel')
plt.legend()
plt.show()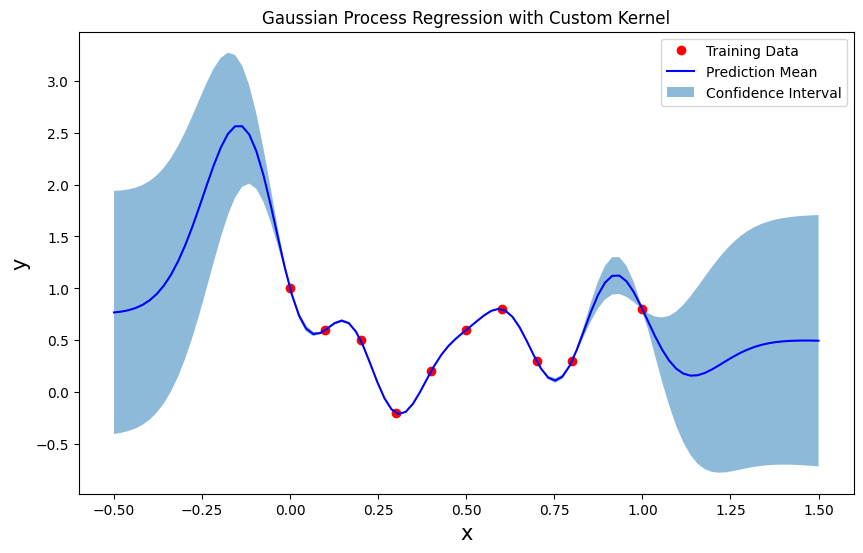
- 가우시안 프로세스 회귀는 학습 데이터가 있는 영역에서는 매우 좋은 예측 성능을 보이며, 데이터가 없는 영역에서는 불확실성이 커지는 특징을 가집니다.
- 신뢰 구간을 통해 모델의 예측에 대한 신뢰성을 확인할 수 있으며, 이는 새로운 데이터에 대해 불확실성을 정량적으로 표현하는 데 유용합니다.
- 커널 함수와 하이퍼파라미터는 모델이 입력 데이터의 패턴을 어떻게 학습하는지에 큰 영향을 미칩니다. 주어진 하이퍼파라미터 조합에서 모델은 학습 데이터를 잘 반영하고 있으며, 특히 비선형적인 특성을 잘 학습하고 있습니다.
Sample from conditional Gaussian
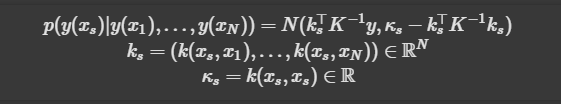
N_sample = 30
ys = np.random.multivariate_normal(mean_ftn.ravel(), cov_ftn, N_sample)
plt.figure()
for i in range(N_sample):
plt.plot(x_query, ys[i])
plt.scatter(x_train, y_train, c='k', zorder=5)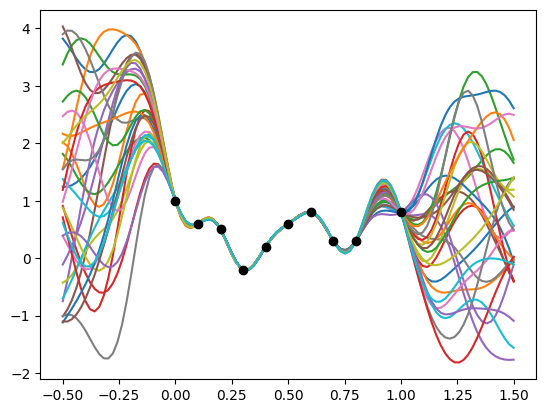
- 이 그림은 가우시안 프로세스 회귀에서 특정 커널을 사용하여 학습된 모델이 불확실성을 표현하는 방식을 잘 보여줍니다.
- 검은 점으로 표시된 학습 데이터는 모델이 정확히 학습한 포인트이며, 이를 기반으로 가우시안 프로세스가 다양한 가능한 함수를 생성합니다.
- 학습된 모델은 학습 데이터 포인트 근처에서는 높은 정확도로 예측할 수 있으며, 학습 데이터가 없는 부분에서는 예측의 불확실성이 증가하여 다양한 곡선이 나타납니다.
- 이와 같은 가우시안 프로세스의 특성 덕분에, 모델은 데이터를 잘 설명하는 다양한 함수들을 고려하며, 이로 인해 모델의 추정 불확실성을 시각적으로 이해할 수 있게 됩니다.
Use different kernel parameter
theta_params = (1.0, 1.0, 0.1, 0.5) # (theta0, theta1, theta2, theta3)
# 예측 수행
mean_ftn, cov_ftn = GPregression(x_train, y_train, x_query, custom_kernel, theta_params)
std = np.sqrt(np.diag(cov_ftn)) # 분산의 제곱근으로 표준 편차 계산
# 결과 시각화
plt.figure(figsize=(10, 6))
plt.plot(x_train, y_train, 'ro', label='Training Data')
plt.plot(x_query, mean_ftn, 'b-', label='Prediction Mean')
plt.fill_between(x_query, mean_ftn.ravel() - std, mean_ftn.ravel() + std, alpha=0.5, label='Confidence Interval')
plt.xlabel('x', fontsize=15)
plt.ylabel('y', fontsize=15)
plt.title('Gaussian Process Regression with Custom Kernel')
plt.legend()
plt.show()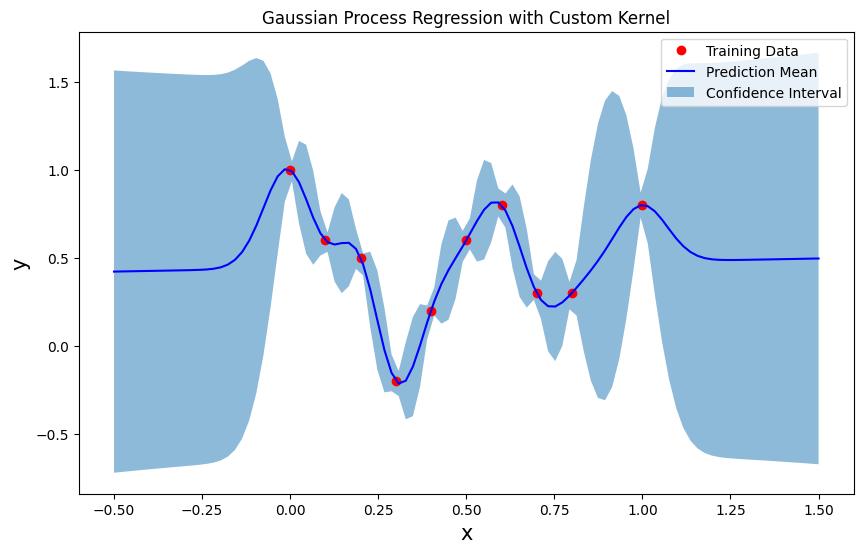
- 학습 데이터가 있는 영역에서는 예측 평균이 데이터를 잘 추종하고 있으며, 신뢰 구간이 좁아 예측의 정확성이 높습니다.
- 반면, 학습 데이터가 없는 영역에서는 예측의 불확실성이 증가하며, 신뢰 구간이 넓어지고 예측 평균도 다양한 변동을 보이는 것을 확인할 수 있습니다.
- 하이퍼파라미터 theta2 의 설정으로 인해 RBF 커널의 폭이 매우 좁아져, 데이터 포인트 간의 영향력이 국소적이며 예측 함수가 급격히 변동하는 것을 볼 수 있습니다. 이는 모델이 국소적인 패턴을 민감하게 학습하고 있다는 것을 의미하며, 새로운 데이터에 대한 일반화가 어려울 수 있음을 시사합니다.
'AI > 대학원' 카테고리의 다른 글
| RNN 의 Parameter Sharing (4) | 2024.11.21 |
|---|---|
| PCA 와 FDA 실습 및 분석 (0) | 2024.11.20 |
| VGG16 을 이용한 Transfer Learning 실습 (4) | 2024.11.11 |
| 도메인에 맞는 AI 지능화 전략 (자율주행 보안) (8) | 2024.11.10 |
| 한양대학교 인공지능융합대학원 25년도 전기 신입생 모집 (11) | 2024.11.07 |



